Language of Mathematics – Concept, Components, and Importance for Teaching Exams


4
Introduction (Exam Perspective)
In teaching aptitude and mathematics pedagogy examinations such as CTET, STET, BPSC TRE, and B.Ed, the language of mathematics is a frequently asked conceptual topic. Mathematics is not only a subject of numbers and calculations; it is a structured language used to express ideas, relationships, and logical reasoning clearly and precisely.
For a teacher, understanding mathematics as a language is essential for effective classroom communication, conceptual clarity, and learner comprehension.
Language and Its Relationship with Academic Disciplines
Language has an intimate relationship with all academic disciplines. Every subject develops its own way of communicating ideas. Mathematics uses symbols, numbers, signs, and structured expressions to convey meaning accurately.
In pedagogy, language is viewed as a systematic and scientific process of exchanging thoughts, emotions, and symbols. Math follows this process in a highly organised and universally accepted form.
Mathematics as a Language
Mathematics has its own independent language. Like spoken or written language, it enables communication, but with greater precision and universality. Mathematical language allows learners and teachers across the world to understand the same concept without ambiguity.
From a teaching-exam viewpoint, mathematics is considered a language because it:
- Uses symbols instead of words
- Follows fixed rules and conventions
- Conveys meaning through structure and logic
- Encourages reasoning rather than memorisation
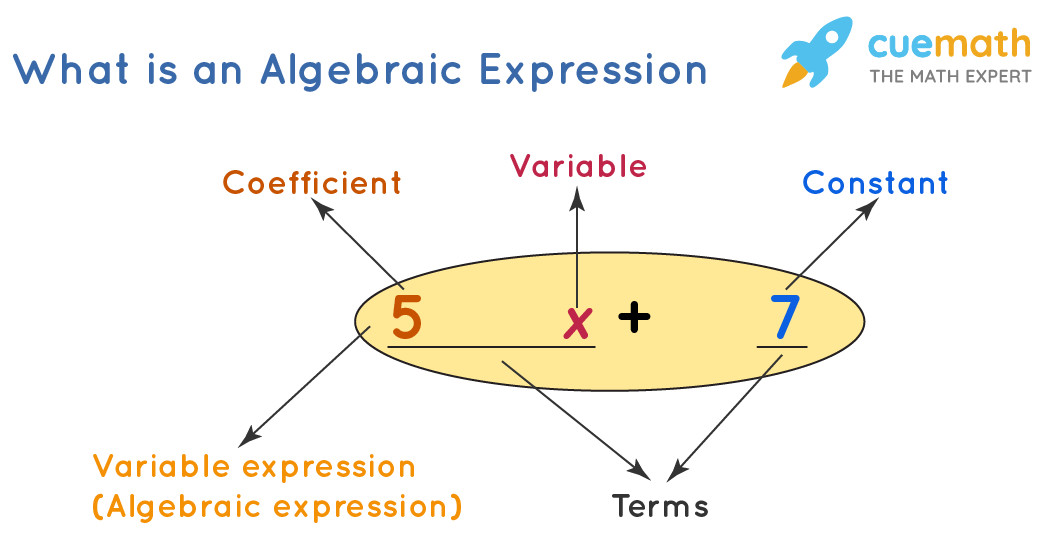
Components of the Language of Mathematics


4
Mathematical Syntax
Syntax refers to the order and arrangement of mathematical symbols and expressions. Just as word order matters in a sentence, symbol order matters in mathematics. Incorrect syntax leads to incorrect meaning, a common source of student errors noted in pedagogy questions.
Mathematical Grammar
Mathematical grammar consists of rules that govern operations and relationships, such as:
- Laws of arithmetic
- Order of operations
- Rules for equations and inequalities
Grammar ensures consistency and correctness in mathematical communication.
Mathematical Vocabulary
Mathematics has a specific vocabulary, where each term has a definite meaning. Words such as variable, factor, equation, function, and theorem cannot be interpreted loosely. In exams, questions often test a teacher’s understanding of correct mathematical terminology.
Mathematical Discourse
Mathematical discourse includes discussion, explanation, justification, and reasoning. Modern pedagogy emphasises encouraging students to:
- Explain how they arrived at an answer
- Use correct mathematical language
- Justify their reasoning logically
This aligns with constructivist and learner-centred approaches, frequently highlighted in CTET and B.Ed syllabi.
Meaning in Mathematics
Symbols in mathematics do not carry meaning by themselves. Meaning develops when learners understand what the symbols represent. For example, the symbol “=” represents equality, not simply an instruction to calculate. Conceptual understanding of meaning is a key focus area in teacher eligibility examinations.
Importance of Mathematical Language for Teachers



4
A teacher’s command over the language of mathematics helps in:
- Developing conceptual understanding among learners
- Reducing mathematics anxiety
- Encouraging logical reasoning
- Improving classroom interaction and explanation
Examination questions often link mathematical language with effective teaching strategies and learner understanding.
Role of the Teacher in Developing Mathematical Language
From an Exam Affinity teaching perspective, the teacher must:
- Use simple and precise mathematical language
- Encourage students to speak and write mathematically
- Connect symbols with real-life contexts
- Promote reasoning over rote calculation
Such practices are aligned with child-centred pedagogy, a core theme in CTET, STET, and BPSC TRE exams.
Exam-Oriented Key Takeaways
- Mathematics is a language of symbols, logic, and structure
- It has syntax, grammar, vocabulary, discourse, and meaning
- Understanding mathematical language improves teaching effectiveness
- Teacher exams emphasise conceptual clarity over computation
- Mathematical language supports reasoning, communication, and understanding