Introduction
Understanding how students learn geometry is essential for effective mathematics teaching. Van Hiele’s Theory of Geometric Thinking, proposed by Pierre van Hiele and Dina van Hiele, explains how learners progress through different levels of geometric understanding. This theory provides valuable insight to teachers about why students struggle with geometry and how instruction should be planned according to the learner’s cognitive level.
According to Van Hiele, students move through five hierarchical levels of geometric thinking, and no level can be skipped. Progression depends on instruction and experience, not age.
Key Assumptions of Van Hiele’s Theory of Geometric Thinking
- Students progress through fixed and sequential levels of geometric thinking
- Each level uses a distinct language, symbols, and reasoning style
- Consequently, students cannot skip any level
- However, proper teaching enables movement from one level to the next
- Thus, memorisation alone never leads to higher-level geometric understanding
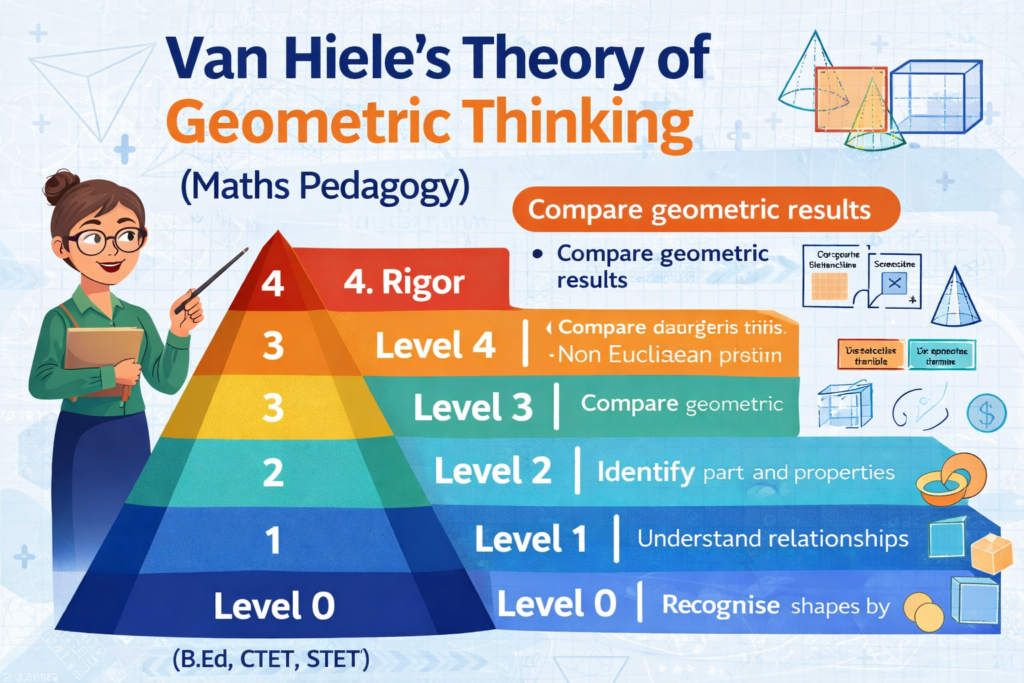
Levels of Van Hiele’s Geometric Thinking
Level 0: Visualisation (Recognition Level)
- At this level, students recognise shapes by their overall appearance
- They identify figures based on visual similarity
- However, they do not understand the properties of shapes
- As a result, rotation or inversion creates confusion
- Learning remains purely visual
Examples
- Students identify a circle as a coin or bangle
- They recognise a square only when it looks exactly like a square
Class Level
- Elementary level classes
Level 1: Analysis
- At this stage, students focus on parts and properties of shapes
- They classify figures using sides and angles
- However, they fail to relate one property to another
- Therefore, logical reasoning remains limited
Examples
- A circle is described as a closed figure with no corners
- A square is identified as a shape with four equal sides
Class Level
- Upper elementary classes
Level 2: Abstraction or Informal Deduction
- At this level, students understand relationships among properties
- Consequently, they classify shapes logically
- Moreover, they participate in informal deductive discussions
- Thus, they recognise inclusion relationships among figures
Examples
- Opposite sides of a rectangle are parallel
- All equilateral triangles are isosceles
- A square shares properties with a rectangle
Class Level
- Upper elementary to secondary level
Level 3: Deduction or Formal Deduction
- At this stage, students understand definitions, axioms, and theorems
- They apply logical reasoning systematically
- As a result, they write step-by-step proofs
- Therefore, geometry becomes a structured logical system
Examples
- Students prove that a square is a rectangle
- They explain why a rectangle is not necessarily a square
Class Level
- Secondary school level
Level 4: Rigor
- At this highest level, students analyse different geometric systems
- They compare axiomatic structures logically
- Moreover, they study geometry beyond Euclidean assumptions
- Thus, abstract reasoning reaches maturity
Non-Euclidean Geometry
- Non-Euclidean geometry refers to any geometry in which Euclid’s fifth postulate does not hold
Euclid’s Fifth Postulate
- Through a point outside a line, only one line can be drawn parallel to the given line
Class Level
- Senior secondary and university level
Educational Importance of Van Hiele’s Theory
- This theory helps teachers identify students’ thinking levels
- Therefore, it supports meaningful geometry learning
- Moreover, it guides teachers in choosing appropriate strategies
- Consequently, it discourages rote memorisation
- Thus, it promotes activity-based and conceptual learning
Implications for Teaching Geometry
- Teachers should first identify the learner’s Van Hiele level
- Then, they should plan instruction accordingly
- Visual activities should dominate lower levels
- Gradually, reasoning and proof should receive emphasis
- Hence, teaching must progress from concrete to abstract
Conclusion
- Van Hiele’s Theory offers a clear pedagogical framework for geometry teaching
- It shows that understanding develops systematically
- Therefore, effective teaching requires alignment with learners’ thinking levels
- Hence, the theory holds great importance for B.Ed, CTET, STET, and teaching exams